Home

Research

PETER J. BADDOO

1993 - 2023

Welcome to Peter’s academic website.

Peter was an applied mathematician at MIT. His main research interests were:

•   Complex function theory
•   Fluid dynamics
•   Machine learning and data-driven methods

BIO

Peter was an Instructor in Applied Mathematics at MIT. Previously he was an EPSRC Doctoral Prize Fellow in the Department of Mathematics at Imperial College London. He completed his PhD in July 2019 in the Department of Applied Mathematics and Theoretical Physics at the University of Cambridge. Prior to that, he completed a four-year MMath at the University of Oxford.

Sadly, Peter died suddenly of a cardiac arrest in February 2023 whilst playing basketball. He is dearly missed by family, friends and colleagues, but we hope his academic research continues to inspire others.

Peter helped bring people together in his various communities. In his honour, the Department of Mathematics at MIT endowed the Peter Baddoo Community Building Award to recognise outstanding contributions to community-building within the department.

Peter was originally from Reading, UK. Beyond research, his interests were sports, music and theology.

SELECTED PAPERS

Here are three selected papers Peter worked on :

•   2023: "Physics-informed dynamic mode decomposition (piDMD)" (link, video)

            P. J. Baddoo, B. Herrmann, B. J. McKeon, J. N. Kutz & S. L. Brunton

•   2022: "Generalization of waving-plate theory to multiple interacting swimmers" (link, video)

           P. J. Baddoo, N. J. Moore, A. U. Oza & D. G. Crowdy

•   2021: "Log-lightning computation of capacity and Green's function" (link, video abstract)

            P. J. Baddoo & L. N. Trefethen, Maple Transactions

You can view a more complete list here.

MISCELLANY

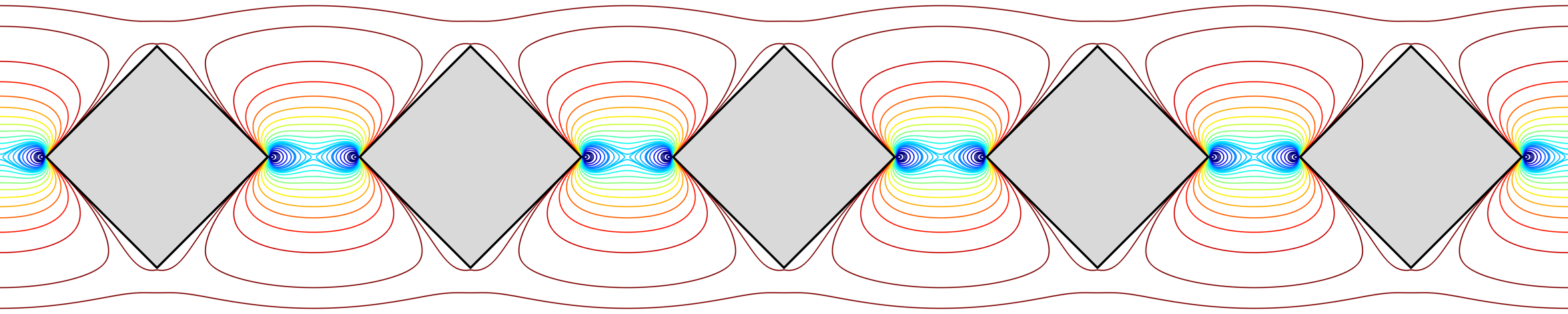
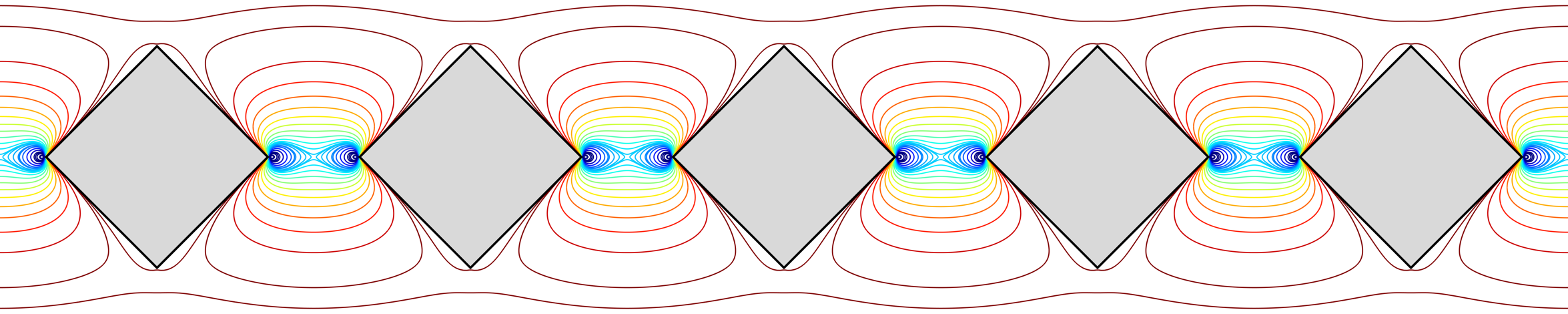
The image in the header and footer is an illustration of the trajectories of point vortices embedded in a potential flow with a periodic array of obstacles. The dynamical system can be expressed in a conservative form which leads to a Hamiltonian that describes the vortex paths. The colours denote the energy of each configuration: red means highly energetic states whereas blue corresponds to states with low interaction energy. Analytic expressions for the trajectories are available in a canonical circular domain which is then mapped to the physical domain using a new periodic Schwarz–Christoffel mapping formula.

If you came here looking for a dating website, you'd be better off at www.badoo.co.uk (one "d")